分子动力学模拟(一)
随着化学、生物学等相关实验技术的迅猛发展,越来越多的生物大分子结构被解析完全,为从分子层面探究人体生理生化反映,疾病的发病机制以及药物的药理作用等奠定了坚实的基础。但受到各种实验方法的限制,解析所得的结构基本为静态结构。而生物大分子在行使其生物学功能时,往往是一个动态过程,这些复杂分子的动态性质又很难通过实验的技术准确测定。加之,生物体内的固有无序蛋白(intrinsically disordered protein)由于没有稳定的高级结构,尚且无法通过实验的方法进行结构解析。这些也是从事药物设计工作的研究人员不得不面对的难题。
1976年,Warshel A.与Levitt M. 应用量子力学(quantum mechanics, QM)理论,通过计算模拟研究了酶分子活性部位在化学反应中的电子转移,堪称计算机模拟技术在生命科学中应用的先驱性工作之一。一年后,Karplus M.首次使用分子动力学模拟(molecular dynamics, MD)从原子水平对蛋白质分子的动力学行为进行探究,并初步建立了蛋白质的分子力场(force field)和MD模拟程序。为解决实验无法精准测定生物大分子动态行为的难题指出了新的方向。为了奖励他们三人在发展复杂化学与生物学体系多尺度模拟方面所做的贡献,他们共享了2013年诺贝尔化学奖。
时至今日,经过近40年的发展,MD模拟已能够处理复杂的生物大分子体系及生理过程,尤其是在蛋白质结构-功能研究领域具有显著优势。并衍生出了拉伸分子动力学(steered molecular dynamics, SMD)模拟、非平衡态分子动力学模拟等多种理论和方法。现在,MD模拟程序大多已经商业化,常见的专业软件有:AMBER、NAMD、GROMACS等。
分子动力学模拟的原理
MD模拟是一种采用经典分子力学(molecular mechanics, MM)方法的模拟技术。经典MM方法是指应用谐振子模型、库伦静电模型等经典物理模型描述,模拟生物大分子的方法。在MM方法模拟分子体系的过程中:体系被视为由刚性的球状原子构成,且每个原子具有特定的范德华(van der Waals)半径、极化率(polarizability)及电荷;原子间的相互作用被分为化学键作用和非键作用,并使用力场函数和参数表示,而力场函数与参数则通过实验数据及量化计算结果拟合得到。因为在室温条件下,对于由成千上万个原子构成的生物大分子体系来说,一般的量子效应可以忽略不计(酶反应等量子效应较为明显的情况除外)。这种含有实验数据拟合成分的半经验模型具有原理简单,计算效率高等特点,较为适合处理组成复杂的生物大分子体系。
生物大分子的经典力学模型
根据统计力学的观点,实验观测的宏观物理量可用系综(ensemble)的平均值来描述。系综定义为一定宏观条件下,大量性质和结构完全相同,处于各种运动状态且各自独立的系统微观运动状态的集合。假定一个孤立体系从任一初态出发,经过足够长时间的演变后将历经一切可能的微观状态,则该体系处于平衡态的宏观性质就相当于微观量在足够长时间内的平均值,即该平衡态的系综统计平均值。对于一个由N个原子组成的体系,其力学量A的系综平均值如式1所示:
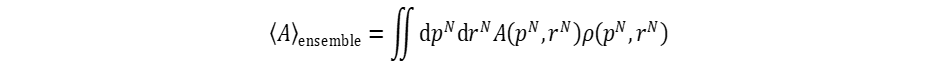
(1)
在通常实验条件下,体系是可与环境这个大热源进行热交换而达到热平衡的封闭体系,其统计分布可由正则系综(canonical ensemble, NVT)表示。NVT系综的概率密度为如式2所示:
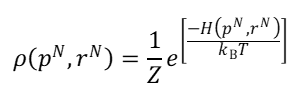
(2)
式2中,H表示体系的哈密顿量(Hamiltonian);T为热力学温度;kB表示玻尔兹曼常数,Z为配分函数(partition function):
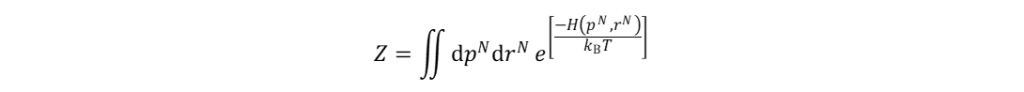
(3)
配分函数中的积分须包括体系所有可能的围观状态。常用的MD模拟是通过牛顿运动定律求解体系中N个相互作用原子在相空间内随时间变化的一系列微观运动状态,从而获得体系中每个原子的坐标轨迹、速度轨迹和体系的能量轨迹。而体系中原子间的相互作用及体系的势能则通过分子力场定义。这些运动状态分别对应于分子体系在特定热力学状态下的各个构象,因此可以视为是对分子体系在该热力学状态下系综的采样。因此,根据MD模拟的结果,体系的热力学量和其他宏观性质均可通过系综平均计算得到。值得一提的是,在MD模拟中力学量可表示为微观状态对时间的积分,避免了较难计算的配分函数项(式4):
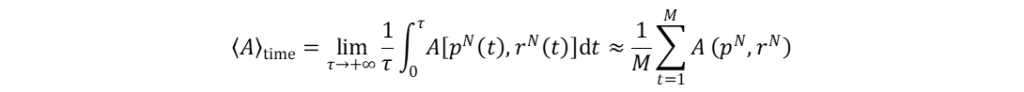
(4)
在式4中,t表示模拟时间;M表示MD采样的轨迹数。从式4可以看出,只有当MD模拟对相空间进行了充分的采样,约等号右边的平均值才近似于左边的系综平均值。而能否充分采样则与可用计算资源的多少有关。