分子动力学(三)
四、周期性边界条件
在MD模拟过程中,为了尽可能多的提高计算精度,而将具有周期性的物理问题简化为周期性单元处理,并引入周期性边界条件(periodic boundary condition)消除边界效应对小尺度模拟体系产生的影响。例如:立方体盒子周期性边界条件是以立方体为基本单元,生物大分子体系及环境(溶剂等)位于该基本单元中。通过无限次复制平移,让基本单元周围充满“镜像”,且每个单元的边界都是开放的,单元中的粒子可以自由进出(图1)。在模拟过程中,如果基本单元中的一个粒子逃出了单元边界,则该粒子的镜像就会从反方向的边界以相同的速度进入该单元。这样就消除了边界,搭建了一个准无穷大的空间体积。周期性边界条件中常见的基本单元的形状除了立方体盒子外,还有单斜体盒子、去头八面体(truncated octahedron)盒子等。
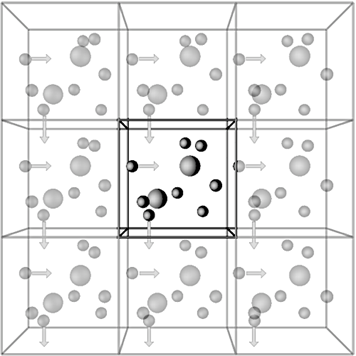
图1 周期性边界条件
在设定周期性边界条件时,为保证模拟的少量原子所受到的力与处于大环境中的原子所受到的力相当,那么基本单元的边长应至少大于截 > 断距离(cutoff distance)rcut的两倍。rcut是在模拟过程中,计算原子间相互作用力时,假设相互作用是短程,为了减少计算量而设定的阈值。即当原子i与原子j间的距离超过rcut(rij > rcut),原子i与原子j之间的相互作用可以忽略不计。在计算粒子间的相互作用时,常使用“最小像力约定(minimum-image convention)”。最小像力约定是指在无穷重复的MD基本单元中,假设单元内有n个粒子,每个粒子只同基本单元内的另外n-1个粒子或其相邻最近的镜像粒子发生相互作用。
五、SHAKE约束条件
为了提高模拟时的计算效率,防止生物大分子结构崩塌,通常要使用约束条件对分子内高频振动的化学键进行约束。例如:为了保持氢原子参与形成的化学键的能量守恒,需要0.5 fs的模拟时间步长。如果引入约束条件固定键长,即可使用2 fs的时间步长,从而显著提高模拟效率,降低计算成本。
SHAKE算法是常用的约束条件方法,它通过给定的约束距离来保持化学键的几何构型。如:一组原子坐标ri经过无约束模拟的一个时间步长后生成一组新的坐标ri’,根据给定的距离约束条件,SHAKE算法把ri’转化为一组满足条件的ri’’。应用于Verlet积分算法时,SHAKE根据约束条件计算一系列的约束力,使在每一模拟步长结束时满足给定的约束条件。为求解拉格朗日乘子,SHAKE通过迭代法对一组耦合的约束方程依次求解,直至收敛至设定的约束精度。值得注意的是,SHAKE算法无法求解较大的位移。这与SHAKE算法是对耦合的键逐一处理,校正一个键可能会带动其他键产生较大的位移,从而可能造成难以收敛的情况有关。因此,SHAKE算法会设定一个距离偏差范围,如果约束导致的距离偏差超过了设定的范围,则判为计算失败跳出迭代。
六、非键相互作用
在MD模拟中,原子间的在相互作用可分为成键相互作用和非键相互作用。其中,非键相互作用又包括分子内和分子间两种相互作用。具体来说,有静电相互作用、范德华相互作用、π效应和疏水效应(hydrophobic effect)四种。分子内的非键相互作用对维持生物大分子的高级结构具有重要意义,如:疏水效应是蛋白质折叠过程中的重要驱动力,静电、范德华及氢键相互作用是稳定生物大分子高级结构的重要因素。分子间的非键相互作用则在生物分子间相互识别和特异性结合中发挥着重要作用,如:抗体与抗原的识别,酶与底物的结合等。在药学领域中,绝大多数药物通过非键相互作用与生物大分子结合从而调控其功能达到治疗目的。因此,正确处理非键相互作用是MD模拟的关键。在MD模拟中,非键相互作用被分为短程相互作用和长程相互作用分别进行处理。
1. 短程相互作用
上面已经提到,短程相互作用往往是通过设定rcut来处理的。MD模拟计算过程中仅考虑rcut范围内的相互作用,而忽略超出rcut范围的相互作用。尽管这样大大降低了计算量,但检查和计算体系中各原子对间的距离仍然十分耗时。为了进一步加快计算速度,Verlet算法引入了“邻近列表(neighbor list)”的概念检测原子对。邻近列表定义了一个与比rcut稍大的rlist。在开始模拟时,根据r ij < r list ij构建与原子i邻近的原子j的列表。在后续的模拟时间步长内,只需检查当前列表内的原子j即可计算原子i所受的力。邻近列表应频繁地更新以避免列表外的原子进入rcut范围内。
2. 长程相互作用
长程相互作用中,主要考虑范德华相互作用和静电相互作用两项。其中L-J项随距离的增长迅速衰减,看似对长程作用的贡献不显著,但忽略后仍会对体系造成很大误差。对L-J项的处理方式仍然是截断法,并通过引入统一的纠正项补偿截断范围外损失的部分相互作用。
静电相互作用与L-J项不同,是一种衰减缓慢的长程相互作用。这种相互作用在生物体中具有重要作用,MD模拟中必须精确计算。若使用截断法处理静电相互作用会造成系统显著不连续,引起较大误差。精确计算长程静电相互作用需要同时考虑基本单元及其镜像中的原子对,是MD模拟中最消耗计算资源的步骤。1921年,Ewald等提出了Ewald求和法,利用晶体的对称性和倒易空间的原理处理长程静电相互作用,且适用于周期性边界条件,成为计算长程静电相互作用的标准算法之一。由于Ewald法的计算量较大,仅适用于几百个原子的小体系。后来,将Ewald法中耗时的加和方法转换为使用快速傅里叶变换处理,极大提高了计算效率。这种优化算法称为PME(Particle-Mesh-Ewald)方法,现已广泛应用于各种MD模拟的软件包中。Ewald求合法和PME法的详细算法较为复杂,请感兴趣读者参考有关资料,此处不做赘述。