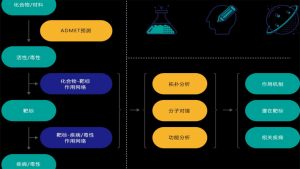
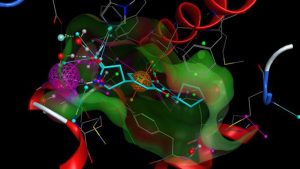
分子动力学是研究分子微观行为的重要现代研究方法之一,其主要方法是依据牛顿运动定律,得出体系分子的运动状态,并对体系进行样本抽取,从而得出相应的构型积分,以进一步得出体系的各种宏观性质。分子动力学模拟在材料、生物、医药等领域有广泛的应用。
起始构型 进行分子动力学模拟的第一步是确定起始构型,一个能量较低的起始构型是进行分子模拟的基础,一般分子的起始构型主要来自实验数据或量子化学计算。在确定起始构型之后要赋予构成分子的各个原子速度,这一速度是根据波尔兹曼分布随机生成的,由于速度的分布符合波尔兹曼统计,因此在这个阶段,体系的温度是恒定的。另外,在随机生成各个原子的运动速度之后须 进 行调整,使得体系总体在各个方向上的动量之和为零,即保证体系没有平动位移。
平衡相 由上 一步 确定的分子组建平衡相,在构建平衡相的时候会对构型、温度等参数加以监控。
生产相 进入生产相之后体系中的分子和分子中的原子开始根据初始速度运动,可以想象其间会发生吸引、排斥乃至碰撞,这时就根据牛顿力学和预先给定的粒子间相互作用势来对各个粒子的运动轨迹进行 计算 ,在这个过程中,体系总能量不变,但分子内部势能和动能不断相互转化,从而 体系的 温度也不断变化,在整个过程中,体系会遍历势能面上的各个点,计算的样本正是在这个过程中抽取的。
计算结果 用抽样所得体系的各个状态计算当时体系的势能,进而计算构型积分。
作用势与动力学计算 作用势的选择与动力学计算的关系极为密切,选择不同的作用势,体系的势能面会有不同的形状,动力学计算所得的分子运动 和 分子内部运动的轨迹也会不同,进而影响到抽样的结果和抽样结果的势能计算,在计算宏观体积和微观成分关系的时候主要采用刚球模型的二体势,计算系统能量,熵等关系时早期多采用Lennard-Jones、morse势等双体势模型,对于金属计算,主要采用morse势,但是由于通过实验拟合的对势容易导致柯西关系,与实验不符,因此在后来的模拟中有人提出采用EAM等多体势模型,或者采用第一性原理计算结果通过一定的物理方法来拟合二体势函数。但是相对于二体势模型,多体势往往缺乏明确的表达式,参量很多,模拟收敛速度很慢,给应用带来很大的困难,因此在一般应用中,通过第一性原理计算结果拟合势函数的L-J,morse等势模型的应用仍然非常广泛。
时间步长与约束动力学 分子动力学计算的基本思想是赋予分子体系初始运动状态之后利用分子的自然运动在相空间中抽取样本进行统计计算,时间步长就是抽样的间隔,因而时间步长的选取对动力学模拟非常重要。太长的时间步长会造成分子间的激烈碰撞,体系数据溢出;太短的时间步长会降低模拟过程搜索相空间的能力,因此一般选取的时间步长为体系各个自由度中最短运动周期的十分之一。但是通常情况下,体系各自由度中运动周期最短的是各个化学键的振动,而这种运动对计算某些 宏观性质 并不产生影响,因此就产生了屏蔽分子内部振动或其他无关运动的约束动力学,约束动力学可以有效地增长分子动力学模拟的时间步长,提高搜索相空间的能力。