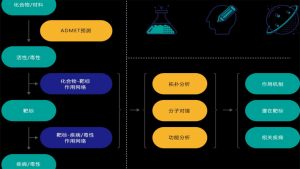
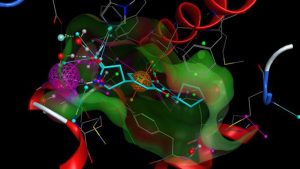
分子模拟名词解释
分子模拟是以计算机为工具,在原子水平上建立分子模型用以模拟分子的结构与行为,进而得出分子体系的各种物理化学性质。
分子模拟常见的模拟方法为分子动力学法(Molecular Dynamics,MD)和蒙特卡洛法(Monte Carlo,MC),
分子动力学法
在分子动力学法中,假设N个粒子(原子、分子或离子)的体系处于一个体积单元(通常为正方体)中,给定每个粒子的初始位置和初始速度,按照一定的时间步长Δt,数值求解牛顿运动方程(球对称分子)或耦合的牛顿-欧拉运动方程(非球对称分子)得出各粒子的运动状态,以得到体系的宏观性质。其中时间步长Δt的选择依赖于体系的温度、密度以及粒子的质量和相互作用势等因素。
蒙特卡洛法
与此不同,在蒙特卡洛法MC中,体系N个粒子的坐标由计算机控制而随机变化,但是此种变化需要满足体系在相空间中每个位形出现的频率与特定统计系综的几率密度成正比。(如,对正则系综,其几率密度为exp (-VN/kT),其中VN为体系势能,k为玻尔兹曼常数,T为温度)这样,便可通过计算机给出的一系列位形的无权重平均得出粒子坐标函数的系综平均。所以,就上述意义讲,在蒙特卡洛模拟中,各个分子坐标的变动不与分子的实际运动联系而没有明确的物理意义。
周期性边界条件
除此之外,实际研究对象的分子数目总要达到1031量级,现如今的计算机不可能模拟如此巨大数目的粒子行为。所以需要引入周期性边界条件,降低计算量。周期性边界条件即去掉周边环境,保持系统不变应该附加的条件。使用周期性边界条件可以做到由部分的性质推广得到全局的性质,即对少量粒子的研究即可得到粒子数巨大的体系的性质。